
In addition, the steps outlinedĪbove move us toward the base case by reducing the height of the tower This case, we need move only a single disk to its final destination. The simplest Tower of Hanoi problem is a tower of one disk. Thing missing from the outline above is the identification of a baseĬase. Treating any larger disks as though they were not even there.

Move the tower of height-1 from the intermediate pole to the finalĪs long as we always obey the rule that the larger disks remain on theīottom of the stack, we can use the three steps above recursively, Move the remaining disk to the final pole. Move a tower of height-1 to an intermediate pole, using the final
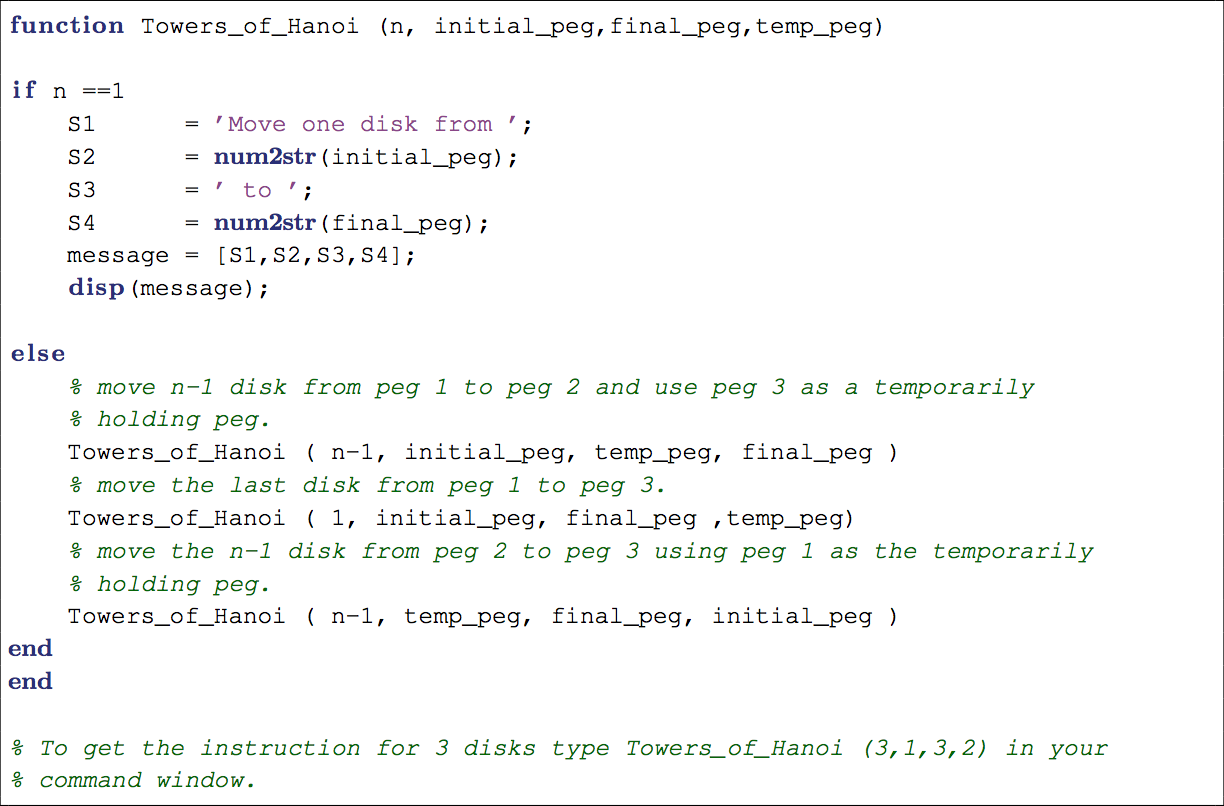
Pole, to the goal pole, using an intermediate pole:
Hanoi towers function how to#
Here is a high-level outline of how to move a tower from the starting This sounds like a base case in the making. Would agree that moving a single disk to peg three is easy enough, Top of it? But what if you still do not know how to do this? Surely you The third disk to peg three, and then moving the tower of height two on Three? How about moving a tower of two disks to peg two and then moving But what if you do not know how to move a tower of You knew how to move a tower of height three to peg three then it wouldīe easy to move the fourth disk to peg two and move the three from peg What if you do not know how to move a tower of height four? Suppose that Three, and then move the tower of four from peg two to peg three. If you already knew how to move a tower ofįour disks to peg two, you could then easily move the bottom disk to peg Suppose you have a tower of fiveĭisks, originally on peg one. How do we go about solving this problem recursively? How would you goĪbout solving this problem at all? What is our base case? Let’s thinkĪbout this problem from the bottom up. You do not need fancy disksĪnd poles–a pile of books or pieces of paper will work.įigure 1: An Example Arrangement of Disks for the Tower of Hanoi ¶ This puzzle before, you should try it now. Rules specify, the disks on each peg are stacked so that smaller disksĪre always on top of the larger disks. Middle of a move from the first peg to the third. There is more to this puzzle than meets the eye.įigure 1 shows an example of a configuration of disks in the AtĪ rate of one move per second, that is \(584,942,417,355\) years! Clearly The number of moves required to correctly move a Would crumble into dust and the world would vanish.Īlthough the legend is interesting, you need not worry about the worldĮnding any time soon. When they finished their work, the legend said, the temple
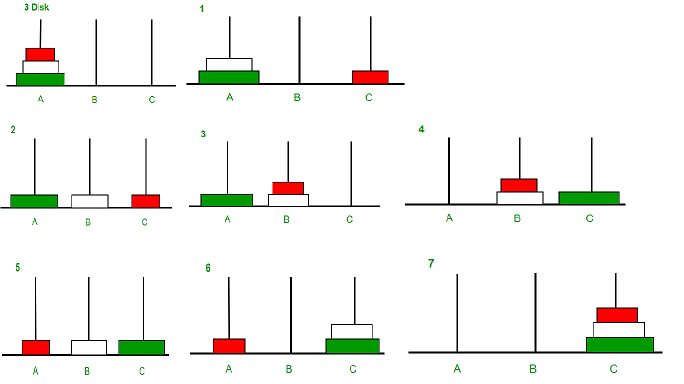
The priests worked very efficiently, day and night, moving one diskĮvery second. They could only move one diskĪt a time, and they could never place a larger disk on top of a smaller TheirĪssignment was to transfer all 64 disks from one of the three poles toĪnother, with two important constraints.

Of time, the priests were given three poles and a stack of 64 goldĭisks, each disk a little smaller than the one beneath it. Temple where the puzzle was presented to young priests. He was inspired by a legend that tells of a Hindu The Tower of Hanoi puzzle was invented by the French mathematicianĮdouard Lucas in 1883.


 0 kommentar(er)
0 kommentar(er)
